
| 제 43강) 정렬 알고리즘 - 힙 정렬3 |
오늘은 정렬 알고리즘의 여섯 번째 시간으로 "힙 정렬"에 대해서 알아봅니다.
드디어 이전에 배운 것들을 가지고 힙 정렬을 시도합니다.
| 힙(Heap) 정렬이란 |
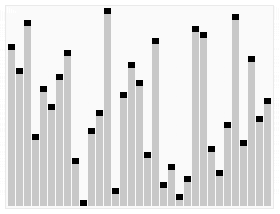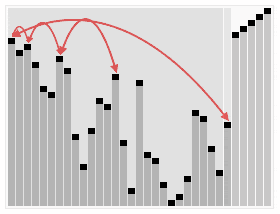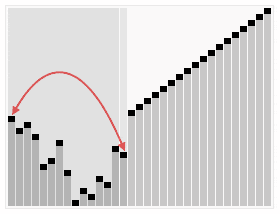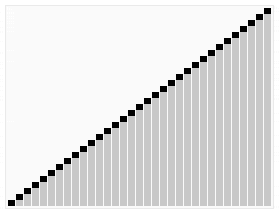
힙은 크게 "Max heap"과 "Min heap"으로 나뉩니다.

"Max heap"(왼쪽)의 경우에는 가장 큰 요소가 맨 위에 올라와 있고, "Min heap"(오른쪽)의 경우에는 가장 작은 요소가 맨 위에 올라와 있습니다.
이렇게 1차적으로 정렬된 힙에서 맨 위의 요소(부모)를 하나씩 제거합니다.
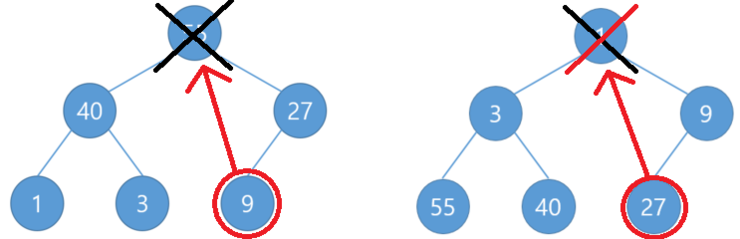
그리고 맨 마지막 요소를 맨 위로 올립니다.

제거한 요소는 새로운 배열에 하나씩 차곡차곡 쌓습니다.

이렇게 바뀐 힙을 다시 재정렬 합니다.

이렇게 재정렬 되어진 힙에서 다시 맨위의 요소를 제거하여 이 과정을 계속 반복합니다.
그럼 결과적으로 새롭게 만들어진 배열에는

이렇게 자연스레 정렬된 배열이 생성됩니다.
"Max heap"을 바탕으로 했다면 내림차순 정렬이, "Min heap"을 바탕으로 했다면 오름차순 정렬이 됩니다.

(그림 출처: 위키 백과 - 힙 정렬)
이렇기 때문에 힙 정렬은 n개의 데이터의 삭제 및 다시 재힙화(heapify) 시간이 포함되어 시간 복잡도는 nlogn이 됩니다.
| 힙 정렬 구현(최대힙 기반) |
그럼 이제 힙 정렬을 구현해보겠습니다.
여기서는 최대 힙(Max heap)을 기반으로 하지만 최소 힙(Min heap)은 최대힙에서 비교연산을 최소비교연산으로 변경만 하면 되기 때문에 직접 구현해보세요.
힙 정렬은 지난 시간에 구현했던 최대 힙에서 3가지만 추가하면 됩니다.
1. 삭제 연산 함수
// 삭제 연산을 담당하는 함수
int delete(Tree* tree)
{
// 트리의 가장 맨 앞 요소(부모)를 임시변수에 저장
int value = tree->arr[1];
// 트리의 가장 맨 앞 요소에 맨 마지막 요소로 바꿈
tree->arr[1] = tree->arr[tree->count];
// 트리의 요소 개수를 1 줄임
tree->count--;
// 힙 재정렬!!
maxHeap(tree, 1, NO);
// 임시변수에 있는 값을 반환!!
return value;
}
2. 힙 정렬 함수 (삭제 연산 + 새로운 배열에 넣는 기능)
// 힙 정렬을 수행하는 함수
void heapSort(Tree* tree, int* sortedArr, int length)
{
for (int i = 0; i < length; i++)
// 삭제연산을 통해 맨 앞요소를 배열에 저장
sortedArr[i] = delete(tree);
}
3. 배열을 출력하는 함수 (선택 사항)
// 배열을 출력하는 함수
void printArr(int* arr, int length)
{
printf("arr: ");
for (int i = 0; i < length; i++)
{
printf("%d", arr[i]);
if (i == length - 1)
printf("\n");
else
printf(", ");
}
}
이리 하여 전체 코드는
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <Windows.h> // Sleep 함수를 위한 헤더파일
#define MAX 100 // 배열의 크기
#define YES 1
#define NO 0
// 트리 구조체
typedef struct _TREE
{
int arr[MAX + 1];
int count;
} Tree;
// 왼쪽 자식의 위치를 계산하는 인라인 함수
inline int leftChild(int index)
{
return index * 2;
}
// 오른쪽 자식의 위치를 계산하는 인라인 함수
inline int rightChild(int index)
{
return index * 2 + 1;
}
// 삽입(항상 맨 끝에 삽입)
void insert(Tree* tree, int value)
{
if ((*tree).count < MAX)
{
(*tree).count++;
(*tree).arr[(*tree).count] = value;
}
else
printf("오류 : 배열 포화 상태");
}
// 두 위치의 값을 바꿈
void swap(Tree* tree, int pos1, int pos2)
{
int tmp = tree->arr[pos1];
tree->arr[pos1] = tree->arr[pos2];
tree->arr[pos2] = tmp;
}
// 최대 힙 함수
// tree: 트리
// pos: 대상 위치
// isSub: 자식 노드와 부모 노드가 스왑된 이후의 최대힙 재계산인지 판단
// YES = 재계산
// No = 일반계산
void maxHeap(Tree* tree, int pos, int isSub)
{
int bigPos = 0; // 자식 노드 중 가장 큰 노드의 위치
int leftPos = 0; // 자식 노드의 왼쪽 노드 위치
int rightPos = 0; // 자식 노드의 오른쪽 노드 위치
// 현재 위치가 0이면 종료
if (pos == 0)
return;
// 왼쪽 자식 노드 위치 계산
leftPos = leftChild(pos);
// 왼쪽 자식 노드가 존재 한다면
if (leftPos <= tree->count)
{
// 오른쪽 자식 노드 위치 계산
rightPos = rightChild(pos);
// 오른쪽 자식 노드도 존재 한다면
if (rightPos <= tree->count)
{
// 큰 노드의 위치를 계산하여 bigPos에 저장
if (tree->arr[leftPos] > tree->arr[rightPos])
bigPos = leftPos;
else
bigPos = rightPos;
}
// 오른쪽 자식 노드가 없다면
// 왼쪽 자식 노드가 자식 노드 중에서 가장 큰 노드
else
bigPos = leftPos;
// 가장 큰 자식 노드와 부모 노드의 대소비교
if (tree->arr[pos] < tree->arr[bigPos])
{
// 부모 노드보다 크면 부모 노드와 해당 자식 노드 스왑
swap(tree, pos, bigPos);
// 스왑되어 바뀐 자식 노드 위치에서 다시 최대 힙 연산 수행
maxHeap(tree, bigPos, YES);
}
}
// 왼쪽 자식 노드가 존재하지 않으면 오른쪽 자식 노드도 존재하지 않음
// 그러므로 종료
else
return;
// 재계산이 아닐경우 다음 부모 노드로 넘어감
if (isSub == NO)
maxHeap(tree, pos - 1, NO);
}
// 삭제 연산을 담당하는 함수
int delete(Tree* tree)
{
// 트리의 가장 맨 앞 요소(부모)를 임시변수에 저장
int value = tree->arr[1];
// 트리의 가장 맨 앞 요소에 맨 마지막 요소로 바꿈
tree->arr[1] = tree->arr[tree->count];
// 트리의 요소 개수를 1 줄임
tree->count--;
// 힙 재정렬!!
maxHeap(tree, 1, NO);
// 임시변수에 있는 값을 반환!!
return value;
}
// 힙 정렬을 수행하는 함수
void heapSort(Tree* tree, int* sortedArr, int length)
{
for (int i = 0; i < length; i++)
// 삭제연산을 통해 맨 앞요소를 배열에 저장
sortedArr[i] = delete(tree);
}
// 트리를 출력하는 함수
void printTree(Tree* tree)
{
printf("tree: ");
for (int i = 1; i <= tree->count; i++)
{
printf("%d", tree->arr[i]);
if (i == tree->count)
printf("\n");
else
printf(", ");
}
}
// 배열을 출력하는 함수
void printArr(int* arr, int length)
{
printf("arr: ");
for (int i = 0; i < length; i++)
{
printf("%d", arr[i]);
if (i == length - 1)
printf("\n");
else
printf(", ");
}
}
int main(void)
{
Tree tree;
const int LENGTH = 18;
tree.count = 0;
int* arr = (int*)calloc(LENGTH, sizeof(int)); // 정렬한 값을 넣어줄 배열
int random;
printf("값 생성: ");
srand((unsigned int)time(NULL));
for (int i = 1; i <= LENGTH; i++)
{
random = rand() % 30 + i;
printf("%d", random);
if (i == LENGTH)
printf("\n");
else
printf(", ");
insert(&tree, random);
Sleep(100); // 최대한 중복값이 생기지 않도록 랜덤값 생성에 텀을 줌
}
printTree(&tree);
maxHeap(&tree, LENGTH / 2, NO); // 시작 지점은 절반 지점
printTree(&tree);
heapSort(&tree, arr, LENGTH); // 힙 정렬!!
printArr(arr, LENGTH);
free(arr);
return 0;
}위와 같습니다.


오늘은 3시간에 걸쳐서 힙 정렬을 배웠습니다.
아주 빠른 정렬 중 하나이자 많이 사용하기 때문에 잘 알아두면 좋습니다.
다음 시간에는 기본적인 정렬 알고리즘의 마지막인 "셸 정렬(Shell Sort)"에 대해서 알아보겠습니다.
'Study > C언어' 카테고리의 다른 글
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 44 [정렬 알고리즘(셀 정렬, Shell sort)] (1) | 2020.05.25 |
|---|---|
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 42 [정렬 알고리즘(힙정렬2 - 힙,Heap)] (0) | 2020.05.25 |
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 41 [정렬 알고리즘(힙정렬1 - 이진트리)] (0) | 2020.05.25 |
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 40 [정렬 알고리즘(퀵 정렬)] (0) | 2020.05.25 |
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 39 [정렬 알고리즘(합병 정렬)] (0) | 2020.05.25 |
