
| 제 41강) 정렬 알고리즘 - 힙 정렬1 |
오늘은 정렬 알고리즘의 세번째 시간으로 "삽입 정렬"에 대해서 알아봅니다.
기본적으로 삽입 정렬은 배열에서 사용합니다.오늘은 정렬 알고리즘의 여섯 번째 시간으로 "힙 정렬"에 대해서 알아봅니다.
힙정렬에 대해서 알기 전에 우리는 "이진 트리"를 먼저 선행학습해야합니다.
그럼 "힙 정렬"의 첫 시간으로 이진 트리부터 알아봅시다.
| 트리란? |
이진트리를 알아보기 전에 트리(Tree)부터 알아봅시다.
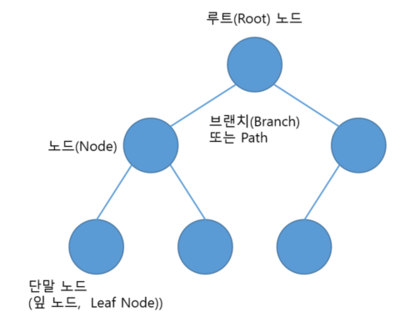
트리란 위와 같이 트리형태(나무모양)의 그래프의 일종으로 각각의 요소를 노드라고 칭하고, 여려개의 노드가 한 노드를 가리킬 수 없는 구조로 되어있습니다.
최상단에 있는 노드를 루트 노드(Root Node)라고 합니다.
맨 아래의, 더 이상의 연결된 요소가 없는 노드를 단말 노드, 혹은 잎 노드(Leaf Node)라고 하며 잎 노드의 상단 노드를 부모 노드(Parent Node)라고 합니다.
단말 노드를 제외한 나머지 노드를 내부 노드(Internal Node)라고 합니다.
노드와 노드를 연결하는 선을 브랜치(Branch) 또는 선, 길(Path)라고 합니다.
| 이진 트리란? |

이진 트리는 위의 그림처럼 한 노드가 최대로 2개의 자식 노드를 갖는 트리를 말합니다.
자식 노드는 왼쪽 노드와 오른쪽 노드로 구분됩니다.
이진트리 단어에 대해서 알아봅시다.
루트 노드에서 자기 자신 노드까지 가는 경로의 길이를 깊이(Depth)라고 합니다.
(루트 노드의 깊이는 0입니다.)
루트 노드에서 자기 자신 노드까지 가는 경로의 길이 + 1을 레벨(Level)이라고 합니다.
(루트 노드의 레벨은 1입니다.)
해당 노드와 잎 노드 사이의 경로의 최대 길이를 높이(Height)라고 합니다.
자기 자신 및 모든 자손 노드의 수를 노드의 크기(Size)라고 합니다.
이진트리는 크게 몇가지의 형태를 갖습니다.
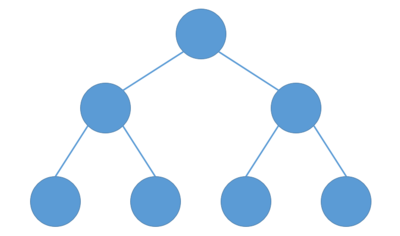
위와 같이 잎 노드를 제외한 모든 부모 노드가 자식을 2갖는, 모든 잎노드의 높이가 같은 트리를 "포화 이진 트리(Full Binary Tree)" 라고 합니다.
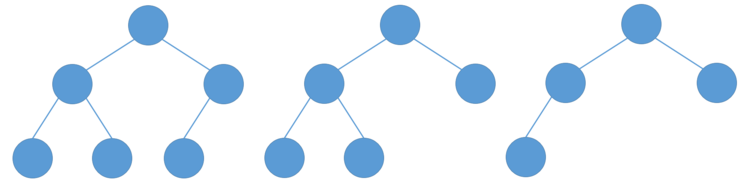
위와 같이 잎 노드들이 왼쪽부터 오른쪽으로 순서대로 채워진 트리를 "완전 이진 트리(Complete Binary Tree)" 라고 합니다.
완전 이진 트리의 경우에는 트리를 배열로 나타내었을때 앞에서부터 차곡차곡 쌓여서 중간에 빈 공백이 없게 됩니다.
(이 이야기는 구현에서 다시 하도록 합시다.)

그러므로 위와 같이 순서대로 채워지지 않은 트리는 완전 이진 트리가 아니게 되는 거죠.

위와 같이 루트노드를 기준으로 왼쪽의 하위트리(부분적으로 만들어진 트리)와 오른쪽 하위트리의 높이차가 1이상 나지 않는 트리를 "균형 트리(Balanced Tree)"라고 합니다.
| 이진 트리 탐색 |
이진 트리의 탐색은 "순회(Traversal)"라는 표현을 사용합니다.
이진 트리는 크게 3가지 방법으로 순회합니다.

먼저 전위 순회(Pre-order Traversal) 입니다.
진행 방향은 "가운데 → 왼쪽 → 오른쪽" 순서입니다.
왼쪽 그림처럼 표현하지만 실질적으로는 오른쪽 그림과 같이 작동합니다.
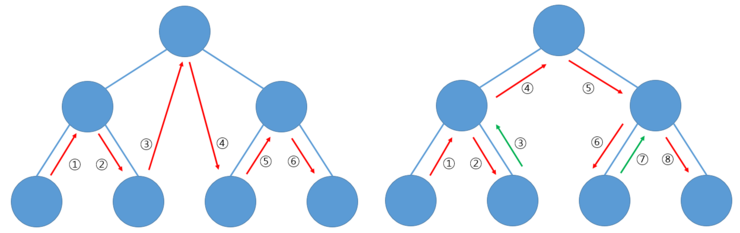
중위 순회(In-order Traversal) 입니다.
진행 방향은 "왼쪽 → 가운데 → 오른쪽" 순서입니다.
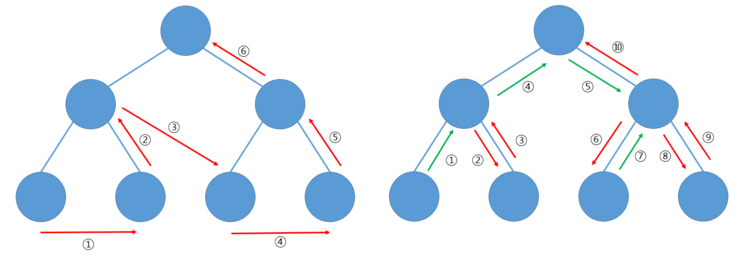
마지막으로 후위 순회(Post-order Traversal) 입니다.
진행 방향은 "왼쪽 → 오른쪽 → 가운데" 순서입니다.
| 이진 트리 구현 |
이제 이진 트리를 구현해봅시다.
이진트리는 기본적으로 2가지 방법을 사용합니다.
배열을 사용하는 방법과 포인터를 사용하는 방법이 있습니다.
배열을 사용하는 방법은 다음과 같습니다.
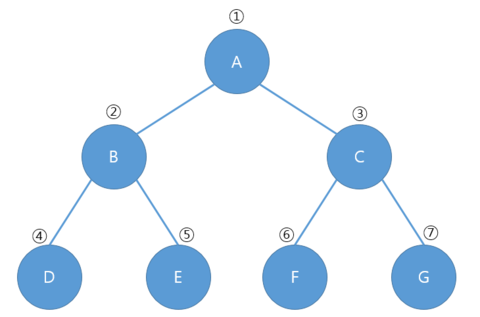
(번호는 배열의 인덱스, 알파벳은 값)
먼저 규칙을 찾아야 합니다.
배열로 트리를 구현할 때는 첫번째 인덱스인 0부터 시작하는 것이 아닌 두번째 인덱스인 1부터 시작하게 됩니다.
그러므로

배열은 다음과 같이 됩니다.
여기서 루트 노드(1)의 자식은 2와 3위치에 있습니다.
노드 B(2)의 자식은 4와 5위치에 있습니다.
노드 C(3)의 자식은 6과 7위치에 있습니다.
그러므로 다음과 같은 공식이 성립됩니다.
| 부모노드(N)의 자식 왼쪽 자식 : 2 * N 오른쪽 자식 : 2 * N + 1 |
이 공식을 활용하여 자식을 찾으면 됩니다.
그럼 배열로 한 번 만들어 봅시다.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 100 // 배열의 크기
// 출력할 때 구분하기 위한 매크로
#define PREORDER 0 // 전위 순회
#define INORDER 1 // 중위 순회
#define POSTORDER 2 // 후위 순회
#define NORMAL 3 // 일반 출력
// 트리 구조체
typedef struct _TREE
{
int arr[MAX + 1];
int count;
} Tree;
// 왼쪽 자식의 위치를 계산하는 인라인 함수
inline int leftChild(int index)
{
return index * 2;
}
// 오른쪽 자식의 위치를 계산하는 인라인 함수
inline int rightChild(int index)
{
return index * 2 + 1;
}
// 전위 순회
void preorder(Tree tree, int index)
{
if (tree.count < index) // 현재 탐색하려는 인덱스가 트리의 인덱스 범위를 넘어서면 탈출
return;
printf("%d ", tree.arr[index]); // 가운데
preorder(tree, leftChild(index)); // 왼쪽
preorder(tree, rightChild(index)); // 오른쪽
}
// 중위 순회
void inorder(Tree tree, int index)
{
if (tree.count < index) // 현재 탐색하려는 인덱스가 트리의 인덱스 범위를 넘어서면 탈출
return;
inorder(tree, leftChild(index)); // 왼쪽
printf("%d ", tree.arr[index]); // 가운데
inorder(tree, rightChild(index)); // 오른쪽
}
void postorder(Tree tree, int index)
{
if (tree.count < index) // 현재 탐색하려는 인덱스가 트리의 인덱스 범위를 넘어서면 탈출
return;
postorder(tree, leftChild(index)); // 왼쪽
postorder(tree, rightChild(index)); // 오른쪽
printf("%d ", tree.arr[index]); // 가운데
}
void traversalMode(Tree tree, int mode)
{
printf("순회 방식: ");
switch (mode)
{
case PREORDER:
printf("전위\nTree: ");
preorder(tree, 1);
break;
case INORDER:
printf("중위\nTree: ");
inorder(tree, 1);
break;
case POSTORDER:
printf("후위\nTree: ");
postorder(tree, 1);
break;
}
}
void printTree(Tree tree, int mode)
{
if (mode == NORMAL)
{
printf("Tree: ");
for (int i = 1; i <= tree.count; i++)
{
printf("%d ", tree.arr[i]);
}
}
else
traversalMode(tree, mode);
printf("\n\n");
}
void insert(Tree* tree, int value)
{
if ((*tree).count < MAX)
{
(*tree).count++;
(*tree).arr[(*tree).count] = value;
}
else
printf("오류 : 배열 포화 상태");
}
int main(void)
{
Tree tree;
tree.count = 0;
srand((unsigned int)time(NULL));
for (int i = 1; i <= 7; i++)
insert(&tree, rand() % 20 + i);
printTree(tree, NORMAL);
printTree(tree, PREORDER);
printTree(tree, INORDER);
printTree(tree, POSTORDER);
return 0;
}소스는 이렇습니다.

포인터를 사용하는 방법은 다음과 같습니다.

노드라는 구조체를 만들어서 안에 값, 왼쪽을 가리키는 노드 포인터, 오른쪽을 가리키는 노드 포인터를 만듭니다.
현재 만드는 이진트리는 정렬기능이 없는 일반적인 이진트리이기 때문에 직접 포인터를 연결하는 방식으로 합시다.
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX 7
// 출력할 때 구분하기 위한 매크로
#define PREORDER 0 // 전위 순회
#define INORDER 1 // 중위 순회
#define POSTORDER 2 // 후위 순회
// 노드 구조체
typedef struct _NODE
{
int value; // 값
struct _NODE* left; // 왼쪽 노드
struct _NODE* right; // 오른쪽 노드
}Node;
// 트리 구조체
typedef struct _TREE
{
struct _NODE* root; // 루트 노드
} Tree;
// 전위 순회
void preorder(Node* node)
{
if (node == NULL) // 현재 탐색하려는 노드가 없다면 탈출
return;
printf("%d ", node->value); // 가운데
preorder(node->left); // 왼쪽
preorder(node->right); // 오른쪽
}
// 중위 순회
void inorder(Node* node)
{
if (node == NULL) // 현재 탐색하려는 노드가 없다면 탈출
return;
inorder(node->left); // 왼쪽
printf("%d ", node->value); // 가운데
inorder(node->right); // 오른쪽
}
void postorder(Node* node)
{
if (node == NULL) // 현재 탐색하려는 노드가 없다면 탈출
return;
postorder(node->left); // 왼쪽
postorder(node->right); // 오른쪽
printf("%d ", node->value); // 가운데
}
void traversalMode(Tree tree, int mode)
{
printf("순회 방식: ");
switch (mode)
{
case PREORDER:
printf("전위\nTree: ");
preorder(tree.root);
break;
case INORDER:
printf("중위\nTree: ");
inorder(tree.root);
break;
case POSTORDER:
printf("후위\nTree: ");
postorder(tree.root);
break;
}
}
void printTree(Tree tree, int mode)
{
traversalMode(tree, mode);
printf("\n\n");
}
// 노드를 만들어주는 함수
Node* createNode(int value)
{
Node* node = (Node*)malloc(sizeof(Node));
node->value = value;
node->left = NULL;
node->right = NULL;
return node;
}
int main(void)
{
Tree tree;
Node* nodes[MAX];
srand((unsigned int)time(NULL));
for (int i = 0; i < MAX; i++)
nodes[i] = createNode(rand() % 20 + i);
// 노드를 직접 연결해줍시다.
nodes[1]->left = nodes[3];
nodes[1]->right = nodes[4];
nodes[2]->left = nodes[5];
nodes[2]->right = nodes[6];
nodes[0]->left = nodes[1];
nodes[0]->right = nodes[2];
// 루트 노드에 연결
tree.root = nodes[0];
printTree(tree, PREORDER);
printTree(tree, INORDER);
printTree(tree, POSTORDER);
// 메모리 해제
for (int i = 0; i < MAX; i++)
free(nodes[i]);
return 0;
}프로그램을 실행해봅시다.
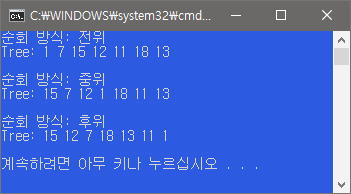
이 결과를 토대로 트리를 그려보면
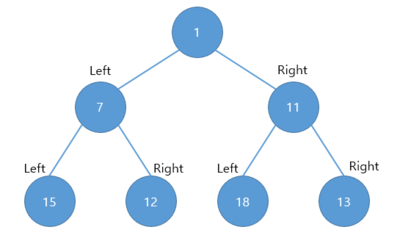
이런 구조를 가진 트리입니다.
오늘은 이진트리에 대해서 알아보았습니다.
다음 시간에는 이 이진트리를 토대로 힙정렬을 배워봅시다.
'Study > C언어' 카테고리의 다른 글
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 43 [정렬 알고리즘(힙정렬3 - 힙정렬)] (0) | 2020.05.25 |
|---|---|
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 42 [정렬 알고리즘(힙정렬2 - 힙,Heap)] (0) | 2020.05.25 |
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 40 [정렬 알고리즘(퀵 정렬)] (0) | 2020.05.25 |
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 39 [정렬 알고리즘(합병 정렬)] (0) | 2020.05.25 |
| 처음하시는 분들을 위한 C언어 기초강의 시즌2 - 36 [정렬 알고리즘(버블 정렬)] (0) | 2020.01.29 |
